함수의 연속성(continuity)과 미분 가능성(Differentiability)
최적화에 들어가기에 앞서 꼭 짚고 넘어가야 할 개념이 있습니다. 혹시 고등학교 때 배웠던 함수의 극한(limit)과 연속(continuous), 기울기(slope)와 도함수(derivative)에 대해 기억나시나요?
알고리즘의 성능을 분석하고 최적화하기 위해서는 기본적으로 함수의 미분 가능성(differentiability)과 연속성(continuity)이 요구됩니다.
함수가 미분이 가능하다면 특정 시점에서 도함수를 구할 수 있고, 함수의 극값을 찾을 수 있습니다. 이를 이용해 알고리즘이 최적해를 찾을 수 있습니다. 그리고 함수가 연속해야만 수렴(converge)할 수 있습니다. 만약 함수가 불연속 하다면 최적화 알고리즘이 잘못된 경로를 따라갈 수도 있고, 최적해(optimal solution)를 찾지 못할 수도 있겠죠.
그렇다면 함수가 미분이 불가능하거나 불연속 하다면 최적화가 어려울까요?
그건 아닙니다. 그리디 알고리즘(greedy algorithm), 근사(approximation) 등 미분과 연속을 요구하지 않는 알고리즘을 이용해 최적화 문제를 풀어나갈 수 있습니다. 이는 추후에 더 자세히 다루도록 하겠습니다.
연속 (Continuous)
연속이란 어떤 함수 f(x)가 어떤 점에서 값이 끊기지 않고, 극한값(limit)이 존재하는 경우를 말합니다.
함수 f(x)가 x=a에서 아래의 조건을 만족한다면 연속이라고 말할 수 있습니다.

아래 그래프에서 어디가 연속일까요?
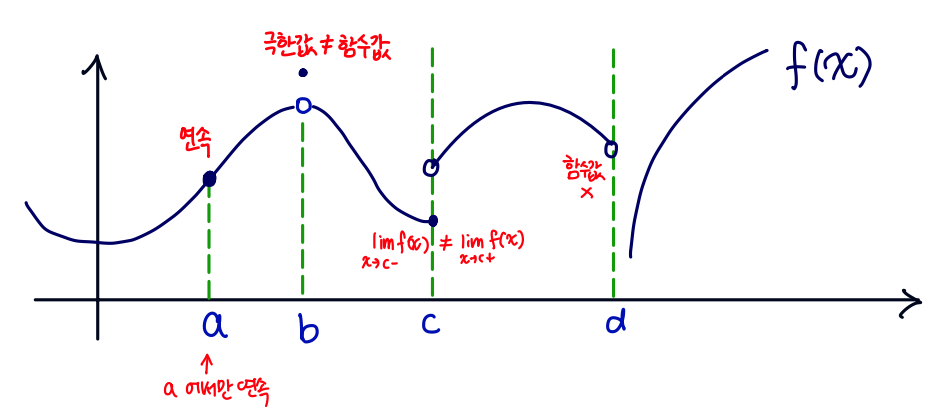
함수의 극한값과 함숫값이 같게 되는 x=a일 때만 연속이 됩니다.
기울기 (Slope)
기울기는 y의 변화량/x의 변화량으로 나타낼 수 있습니다.
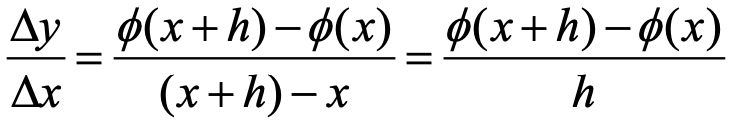
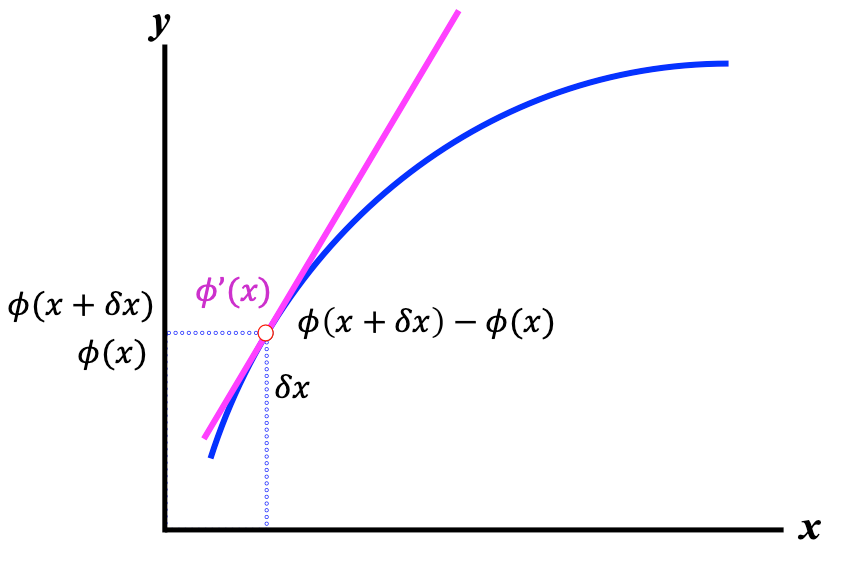
아래 그림에서 빨간 직선에 해당하는 것이 기울기입니다.
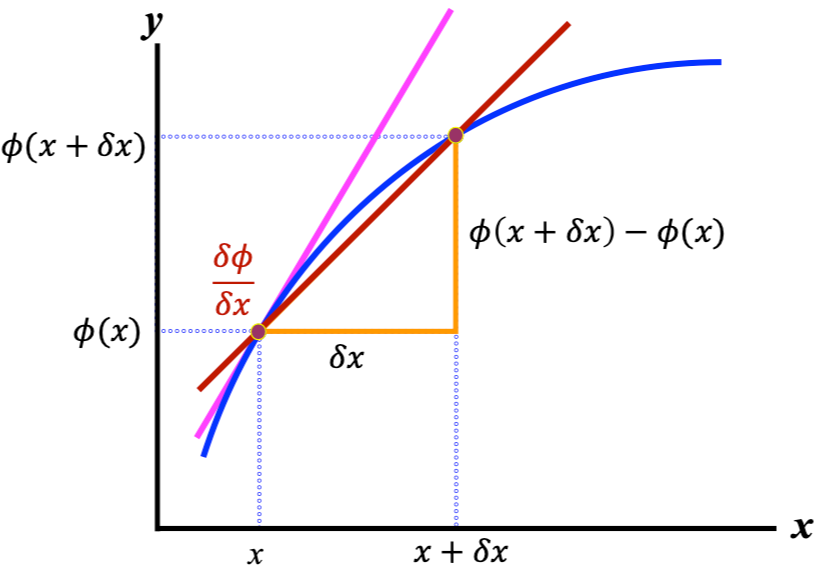
만약 𝛿𝑥가 무한히 작아지면 어떻게 될까요?
x에서의 기울기가 되겠죠. 이게 바로 미분입니다.
최적화에 있어 미분은 계속해서 나오기 때문에 잘 알아두시길 바랍니다.
도함수 (Derivative)
도함수는 함수의 변화량을 나타내는 개념으로 순간의 변화율을 나타냅니다.
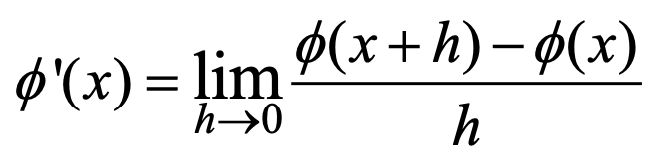
함수 f(x)의 x=a에서의 도함수가 존재하면 f(x)는 x=a에서 미분 가능하다고 합니다. 미분 가능한 함수는 반드시 연속이어야 하는 것은 아니지만, 연속인 함수는 대부분 미분 가능합니다.
1차 미분 (First Derivative), 2차 미분 (Second Derivative)
최적화 문제에서는 1차 미분 외에도 2차 미분과 편미분을 자주 사용하게 됩니다.
2차 미분을 하게 되면 함수의 곡률을 알 수 있기 때문에 곧 다룰 내용인 헤시안 행렬(Hessian Matrix)을 구할 때 사용됩니다.
First derivative (1차 미분)
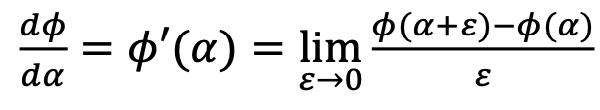
Second derivative (2차 미분)
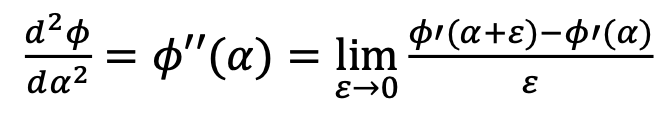
편미분 (Partial Derivative), ∂
∂ : partial (편미분)
최적화 문제에서는 하나가 아닌 여러 변수를 다루는 일이 많습니다. 편미분은 바로 다변수 함수(multivariable function)의 미분을 구하는 방법 중 하나입니다.
편미분은 함수를 각 변수에 대해서만 미분하는 것인데, 이때 다른 변수들은 상수로 취급합니다.
x, y 변수로 이루어진 함수 f(x, y)가 있다고 할 때 x와 y에 대한 편미분의 정의는 다음과 같습니다.
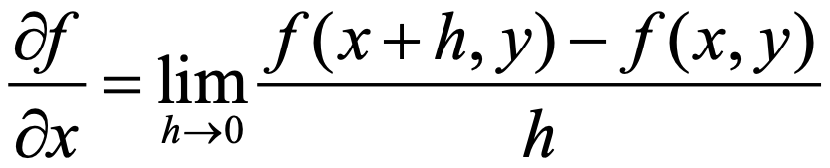
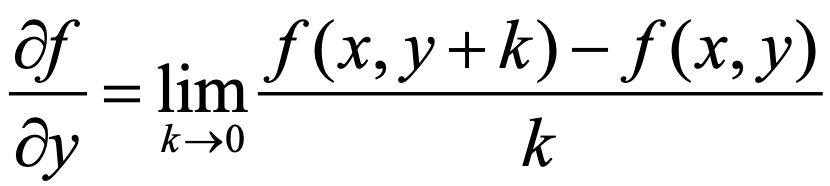
예를 들어 f(x, y)가 이렇게 주어졌다면
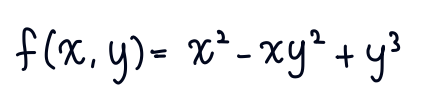
각각의 편미분은 아래와 같습니다.
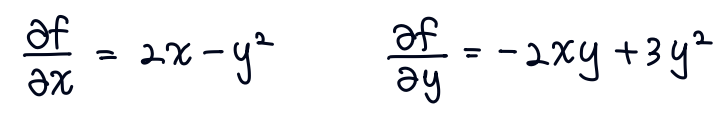
3개의 변수일 때도 각각의 변수에 대해 풀면 됩니다.

함수의 극한과 연속, 기울기와 도함수, 미분과 편미분에 대해 알아보았습니다.

다음에는 그래디언트(Gradient), 헤시안(Hessian), 자코비안(Jacobian) 개념에 대해 알아보도록 하겠습니다.