[Optimization] Unconstrained (제약 조건이 없는 최적화 문제), Local minimum 판단, Critical points, FONC

Unconstrained Optimization : 제약 조건(constraints)이 없는 최적화 문제

 

 

 

제약 조건이 없는 최적화 문제란 변수의 값을 어떤 함수의 최솟값 또는 최댓값으로 만드는 것을 목적으로 하는 문제입니다.

 

변수의 값을 변화시키면서, 목적 함수(objective function)의 값을 최소화 또는 최대화하도록 하는 변수 값을 찾는 것이 목적이죠!

 

이를 위해 다양한 최적화 알고리즘이 사용됩니다. 여기에는 경사하강법으로 많이 들어보셨을 Steepest Descent(Gradient Descent)와 Newton's Method, Quasi-Newton Method 등이 있습니다. 이 알고리즘들은 목적 함수의 값을 최소화/최대화하도록 하는 변수 값의 변화량을 계산하고, 최적해에 근사하는 과정을 반복적으로 수행합니다.

 

 

Theory of Unconstrained Optimization

 

제약 조건이 없기 때문에 최적해가 되는 조건을 제시해 줘야겠죠? 여기에는 FONC라고 일컫는 First-Order Necessary Optimality Conditions와 Second-Order Optimality Conditions가 있습니다.

 

먼저 FONC를 알아볼까요?

 

 

First-Order Necessary Optimality Conditions (FONC)

 

 

 

FONC는 최적해가 되기 위한 필요조건입니다. 최적해가 된다는 것은 그 지점에서 기울기, 즉 gradient가 0이 된다는 것이겠죠? 따라서 아래와 같이 표현할 수 있습니다.

 

   ∇ f(𝑥̅ ) = 0   

∇f(𝑥̅) : 𝑥̅가 최적해일 때 gradient

 

다시 말하면 함수 f가 𝑥̅ 에서 미분가능할 때, 𝑥̅가 local min이라면 ∇f(𝑥̅)=0 이 된다는 거죠.

역은 늘 성립하지는 않습니다. 왜냐하면 local min 외에도 local max, saddle point가 될 가능성도 있기 때문입니다.

 

∇f(𝑥̅)=0

 

 

 

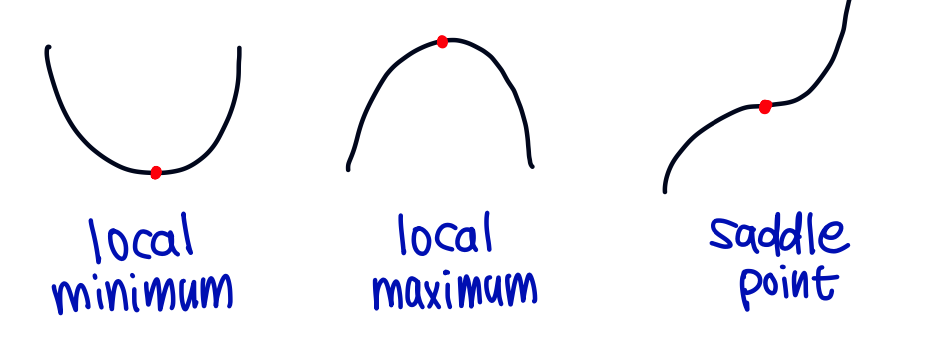
그러면 역이 성립하려면 어떻게 해야 할까요?

바로 Hessian이 PD(Positive Definite)가 되면 되겠죠?

 

여기서 Second-Order Sufficient Conditions(SOSC)가 등장합니다.

 

먼저 SONC부터 알아보겠습니다.

 

 

 

Second-Order Optimality Conditions

 

Second-Order Optimality Conditions는 헤시안 행렬(Hessian matrix)을 통해 최적해를 판단합니다. 헤시안 행렬은 함수를 두 번 미분한 값으로, 함수의 곡률(curvature) 정보를 제공합니다. 따라서 최적해가 되는 지점에서의 함숫값의 곡률 정보를 분석하여, local minimum local maximum, saddle point인지를 판단하는 역할을 합니다.

 

 

Necessary conditions

 

SONC는 함수 f가 𝑥̅ 에서 미분가능할 때, 𝑥̅가 local min이라면

FONC에 의해 ∇f(𝑥̅)=0, SONC에 의해 H(𝑥̅)는 Positive semi-definite가 됩니다.

 

   ∇ f(𝑥̅) = 0  

𝑥̅  :  local min  →  H(𝑥̅):   positive semi-definite  

 

 

이전 포스팅에서 말했던 것처럼 H(𝑥̅)가 positive semi-definite라는 것은 Hessian 행렬의 고윳값(eigenvalue)이 모두 0 이상이라는 뜻입니다. 𝑥̅에서 local minimum이 될 가능성이 있다는 거죠.

 

주의해야 할 것은 𝑥̅가 local minimum이라면 H(𝑥̅)는 positive semi-definite가 되지만 역은 항상 성립하지는 않습니다.

 

 

 

Sufficient conditions

 

SOSC는 함수 f가 𝑥̅ 에서 미분가능할 때, 𝑥̅가 local min이라면

FONC에 의해 ∇f(𝑥̅)=0, SOSC에 의해 H(𝑥̅)는 Positive definite가 됩니다.

 

   ∇ f(𝑥̅) = 0  

𝑥̅  :  local min  →  H(𝑥̅):   positive definite (PD)  

 

 

 

H(𝑥̅)가 positive definite라는 것은 Hessian 행렬의 고윳값(eigenvalue)이 모두 양수라는 뜻입니다. 𝑥̅가 local minimum이라는 거죠. 이 조건은 Second-Order Necessary Conditions보다 강력한 조건입니다.

 

따라서, Second-Order Necessary Conditions은 최적해가 되는 지점에서의 필요조건을 나타내며, Second-Order Sufficient Conditions은 해당 지점이 local minimum 또는 local maximum인지를 판단하는 데 사용되는 충분조건입니다.

 

 

 

Determining Local Optima

 

 

그렇다면 우리가 찾은 포인트가 최솟점(local minimum), 최댓점(local maximum), 안장점(saddle point)인지 어떻게 판단할 수 있을까요?

 

 

 1. Find the Critical points 

 

f(x, y)라는 함수가 주어졌다고 생각해 보겠습니다. 먼저 편미분 값이 0이 되는 critical points를 구합니다.

 

 2. The Second derivative test 

 

다음으로는 행렬식(determinant)을 구합니다.

 

이제 준비가 다 되었습니다!

 

• Local minimum : 최솟값은 고윳값(eigenvalues)이 모두 양수일 때를 뜻한다고 말씀드렸는데요. 방금 구한 Determinant의 부호와 2차 편미분 값의 부호로도 간단하게 판단할 수 있겠죠?

 

• Local maximum : 고윳값이 모두 음수일 때는 최댓값이 됩니다. 

 

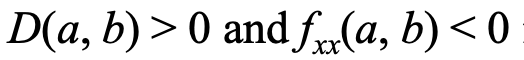
• Saddle point : 행렬식이 음수라면 안장점이 됩니다.

 

 

예제) 다음 함수의 critical points와 local optima를 판단해 보세요.

 

 

 

 

제약 조건이 없는 최적화 문제를 푸는 방법들을 알아보았습니다.

혹시 이해가 안 가는 부분이 있으시다면 댓글을 달아주세요 :)