Gradient, Hessian, Jacobian matrix
최적화에서 중요한 개념인 Gradient, Hessian, Jacobian에 대해 알아보겠습니다. 그 전에 함수의 미분 가능성과 연속성에 대해 기억이 잘 나시지 않는다면 이전 글을 참고해 주세요.
그래디언트(Gradient)
최적화 문제를 효율적이고 안전하게 풀 수 있는 것은 gradient 밖에 없는데요. 이 gradient는 미분의 여러 값입니다. 각 변수에 대해 그 위치에서 1차 미분한 값이죠. 즉 1차 도함수의 벡터값으로, 함수의 각 변수에 대한 변화율을 모아 열벡터(column vector)로 표현한 것입니다.
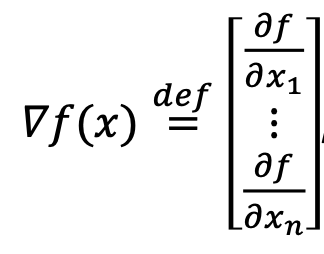
∇f(𝑥)=0이 된다는 것은 그 지점에서의 기울기가 0이라는 것이죠. 즉, 최솟값이나 최댓값을 가질 확률이 높다는 것을 의미합니다. 손실 함수를 최소화하는 최적화 알고리즘에서 최솟값을 찾기 위해서는 결국 gradient, 미분을 사용해서 파라미터 값을 업데이트해야 합니다.
학습에서도 미분값인 gradient가 사용되는데, 이 미분값은 암호와 같은 개념이라 미분값이 공개되면 외부로부터 공격을 받기 쉽기 때문에 보안이 취약해 집니다. 그만큼 gradient는 최적화나 머신러닝에서 굉장히 중요합니다.
헤시안(Hessian), H(𝑥)
헤시안 행렬은 함수를 두 번 미분한 값, 2차 도함수를 행렬로 표현한 것입니다. 이 행렬은 함수의 각 변수에 대한 2차 편미분 값으로 이루어져 있습니다. 헤시안은 대칭 행렬(symmetric)이라는 아주 좋은 성질을 가지고 있죠. 그리고 모든 고윳값이 실수입니다.


예를 들어 아래와 같은 함수의 헤시안 행렬을 구한다고 하면, 대칭 행렬임을 쉽게 알 수 있습니다.
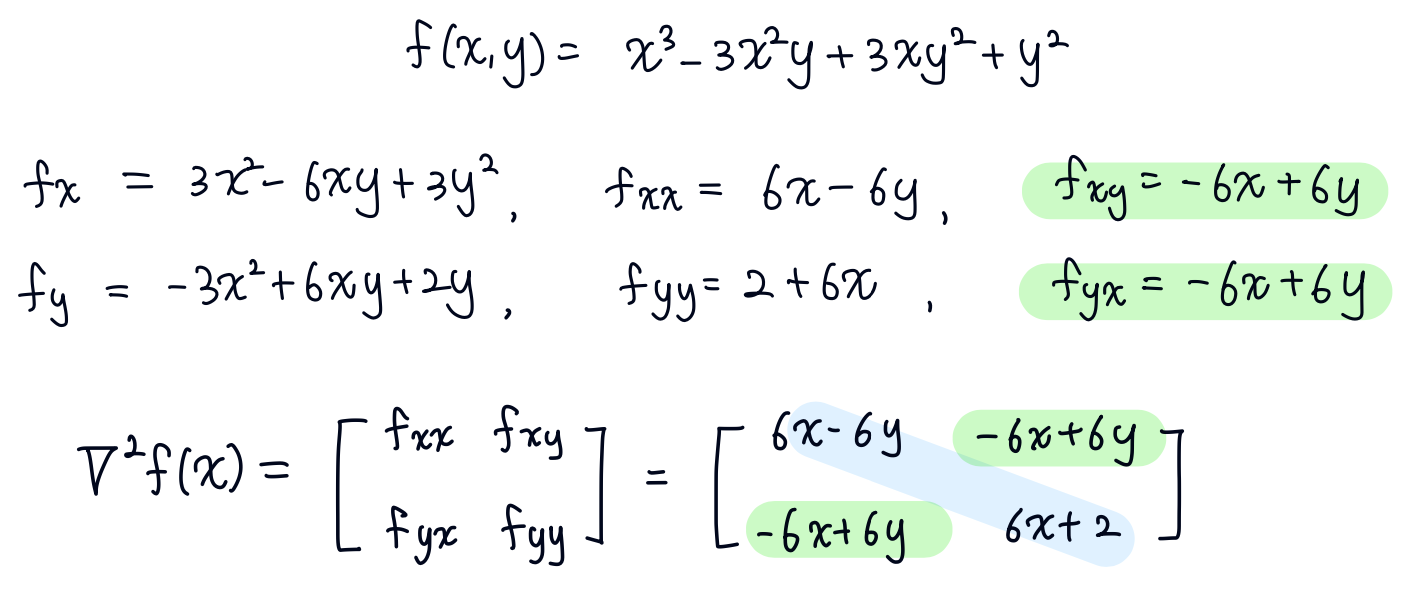
뒤에서 자세히 다루겠지만, 최적화에서 헤시안이 중요한 것은 행렬의 고윳값을 통해 함수의 극값을 판단할 수 있기 때문입니다. 헤시안 행렬의 고윳값(eigenvalue)이 모두 양수라면 local minimum이고, 모두 음수라면 local maximum이 됩니다. 그리고 양수와 음수를 모두 가진다면 saddle point인 것으로 판단합니다.
자코비안(Jacobian)
자코비안/야코비안(Jacobian)은 다변수 함수에서 한 변수가 다른 변수에 따라 변할 때 함수의 변화율을 나타냅니다. 모든 벡터들의 1차 편미분 값으로 된 행렬로 각 행렬의 값은 다변수 함수일 때의 미분값입니다.
벡터 x와 y가 아래와 같이 주어진다면 자코비안은 다음과 같습니다.


예를 들어 y가 2x1 matrix, x가 3x1 matrix라고 할 때, 자코비안 행렬은 아래와 같이 정의됩니다.

다변수 스칼라 함수를 1차 미분하는 그래디언트와 다른 점은 자코비안이 다변수 벡터 함수를 1차 미분한 행렬이라는 점입니다.
Shallow learing에서는 생각할 필요가 없었지만, 딥러닝에서 중요해지는 개념으로 근사(approximation) 접근법을 사용할 때 자주 사용 되는 방법입니다. 다변수 함수의 극값(최댓값 또는 최솟값)을 찾는 최적화 문제에서도 자코비안을 사용합니다. 이때 자코비안은 그래디언트 벡터와 함께 사용되며, 그래디언트 벡터는 자코비안의 전치(transpose)로 정의됩니다.
최적화에서 중요한 개념인 그래디언트, 헤시안, 자코비안에 대해 알아보았습니다.

✓ Gradient : 스칼라 함수에 대한 1차 미분값으로 최적화 알고리즘에서 최솟값을 찾기 위해 사용
✓ Hessian : 2차 미분한 대칭 행렬으로 함수의 극값을 판단하기 위해 사용
✓ Jacobian : 다변수 함수를 1차 미분한 값을 모은 행렬로 근사 접근법에 주로 사용 (딥러닝)
'Data Science > Optimization' 카테고리의 다른 글
| [Optimization] Unconstrained (제약 조건이 없는 최적화 문제), Local minimum 판단, Critical points, FONC (0) | 2023.03.22 |
|---|---|
| [Optimization] 데이터사이언스에서 최적화 개념 (0) | 2023.03.18 |

